THUWC2016 定向越野(markdown 炸了)
题目描述:
题面:
定向越野是一项集智力与体力为一体的体育运动,在这项活动中,选手需要从起点出发,在尽可能短的时间内到达指定的地点。
牛牛非常喜爱这项运动,但是他不知道怎么样才能更快到达终点。他听说来参加集训的你智力过人,于是他把定向越野的地图交给了你,希望你帮他解决一些问题。
牛牛给你的地图描述的是一块平地,地图上不仅清楚地标出了起点和终点的坐标,还标有若干个互不相交圆形区域,每个区域表示一个圆形的水域。对于不会游泳的牛牛来说,进入水域是根本不可能的。因此,牛牛的行动路线不能从水域中穿过。牛牛想知道这样的路线长度最小可以是多少。
输入格式:
第一行包含四个实数 分别表示起点的坐标和终点的坐标。
第二行包含一个整数,表示水域的个数。
接下来行,每行个整数表示一片水域的圆心的,坐标和半径。
保证起点和终点都不在水域的内部或边界上,起点和终点不重合。
输出格式:
输出一行,包含一个实数,四舍五入精确到小数点后恰好1位,表示答案。你的输出必须和标准输出完全一样才算正确。
测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 。
(如果你不知道什么是浮点误差,这段话可以理解为:对于大多数的算法,你可以正常地使用浮点数类型而不用对它进行特殊的处理)
题目链接:http://uoj.ac/problem/277
解题报告:
显然这个是一个圆形障碍最短路的问题;
我们考虑拆点,然后跑最短路算法(dijkstra或者SPFA)。
首先我们要考虑怎么判断,是否存在两点的合法路径,即线段是否与圆相交。
第一点,圆心到直线的距离是否小于圆的半径,显然只有距离小于半径才可能会产生影响。(我们可以使用叉积来判断点到直线的距离)
第二点,圆心在直线的投影点是否在线段上;
也许会有疑问为什么投影点在线段上就存在覆盖,不在线段上就不会覆盖吗?(题面给出是互不相交的圆形区域,那么假如投影点不在线段上并且一个圆形对线段存在覆盖的话,必然会覆盖线段的一个端点,显然与题意不符合,后面会写到线段两个端点的来源)
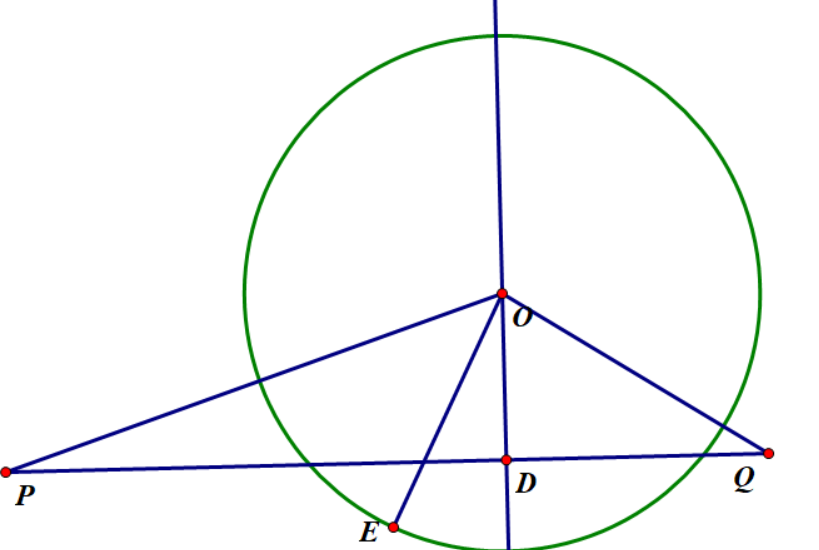
先上图,我们考虑三者长度之间的关系,显然如果在直线上的投影点在线段 那么必然存在并且
然后我们考虑起点和终点与每个圆形的连线
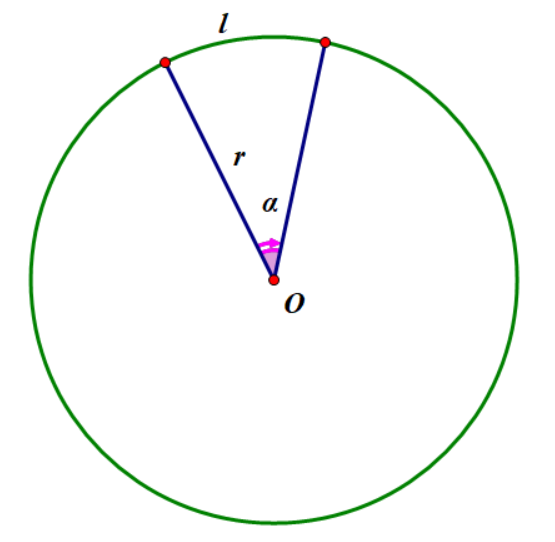
假如要绕过一个圆形障碍的话,必然要从起点或者终点沿着切线走到圆,然后再走一段圆。(显然当一个圆对路径产生影响的时候我们先沿着切线走到圆,然后在走一段圆,再沿着切线走到点是最短的)这时候我们考虑从起点或终点向圆连接切线。
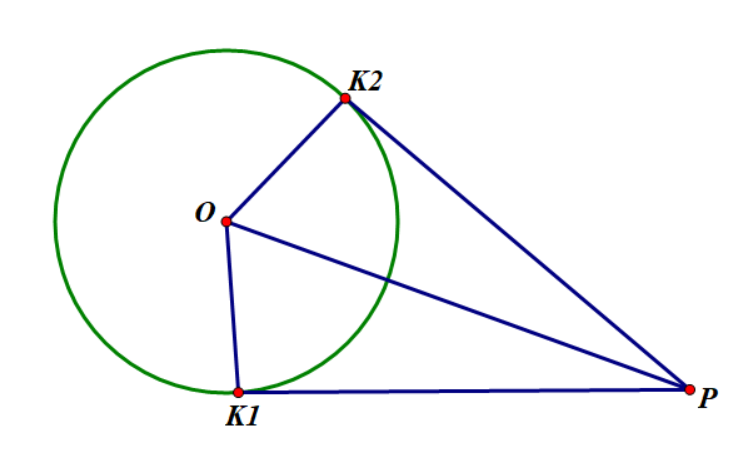
显然
这样我们就能计算角度了
然后我们建立方向上的单位向量,旋转正负角度,就能得到和方向的单位向量了,最后我们从点向他们建边。(当然再计算之前需要判断合法性)
下一步考虑两个圆的连边
与上一步相同,我们可以发现两个圆之间的连线必然是两个圆的内公切线或外公切线。
首先我们考虑两个不相交圆的外公切线
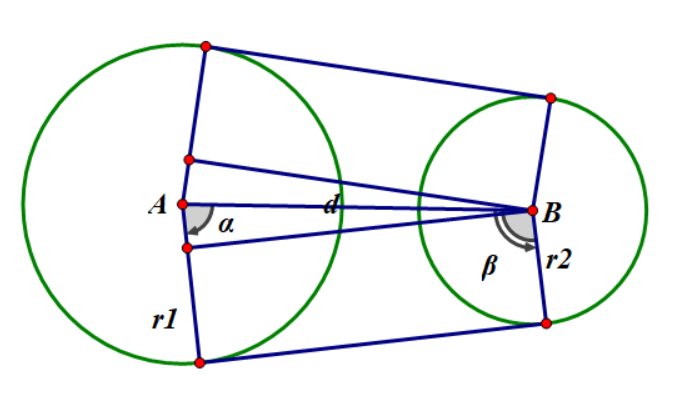
我们需要求的就是和
然后我们考虑他们的内公切线
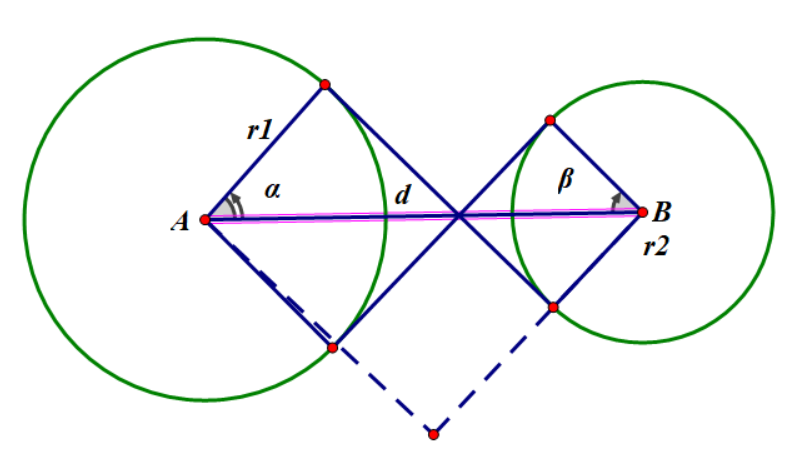
与上面求的类似
假如合法的情况下,我们建立以上四条连边
之后对每个圆上的拆点连边
关于拆点,先前计算的点关于圆心的向量,我们可以使用来记录拆点关于圆心的位置(极坐标)。

然后我们只要把圆上每个相邻的拆点连边就好了。
最后跑最短路即可
代码实现:
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <queue>
using namespace std;
#define I inline
#define R register
#define inf 1073742823
#define FOR(i,begin,end) for(R int i=begin;i<=end;++i)
#define ROF(i,begin,end) for(R int i=begin;i>=end;--i)
const int N = 1000+10;
const int M = 1000000+10;
const double eps=1e-10;
const double pi=acos(-1.0);
#define P point
#define PP const P&
struct point{
double x,y;
I P(const double &_x=0,const double &_y=0):x(_x),y(_y){}
bool operator<(PP a)const{return x<a.x||(x==a.x&&y<a.y);}
I P operator+(PP a)const{return P(x+a.x,y+a.y);}
I P operator-(PP a)const{return P(x-a.x,y-a.y);}
I P operator*(const double a)const{return P(x*a,y*a);}
I P operator/(const double a)const{return P(x/a,y/a);}
I P operator*(PP a)const{return P(x*a.x-y*a.y,x*a.y+y*a.x);}
I double operator|(PP a)const{return x*a.x+y*a.y;}
I double operator&(PP a)const{return x*a.y-y*a.x;}
I double len(){return sqrt(x*x+y*y);}
I double len2(){return x*x+y*y;}
I P rotate(const double theta)const{return P(x,y)*P(cos(theta),sin(theta));}
};
int n;
typedef P vec;
namespace EDGE{
int cnt=1,head[M],idt=2;
struct E{
int to;double v;int nxt;
E(const int &_to=0,const double &_v=0,const int &_nxt=0):to(_to),v(_v),nxt(_nxt){}
}e[1<<22];
I void add(const int &x,const int &y,const double &v){
e[++cnt]=E(y,v,head[x]),head[x]=cnt;
e[++cnt]=E(x,v,head[y]),head[y]=cnt;
}
}
using namespace EDGE;
struct D{
int id;double pos;
I D(const int &_id=0,const double &_pos=0):id(_id),pos(_pos){}
bool operator<(const D&a)const{return pos<a.pos;}
}v[N<<2];
struct C{
P o;double r;int tot,id[N<<2];double pos[N<<2];
I int add(const double t){pos[++tot]=t;return id[tot]=++idt;}
}cir[N],s,t;
P base;
struct T{
P o;double r;int id;
I bool operator<(const T&a)const{return (o-base).len2()<(a.o-base).len2();}
}tmp[N];
I int check(PP p,PP q,int b1=0,int b2=0){
vec v=q-p;
double vlen2=v.len2(),
vlen=sqrt(vlen2),
dis;
FOR(i,1,n)
if(tmp[i].id!=b1&&tmp[i].id!=b2&&
(dis=abs(v&(tmp[i].o-p))/vlen)<tmp[i].r&&
(tmp[i].o-p).len2()<dis*dis+vlen2&&(tmp[i].o-q).len2()<dis*dis+vlen2)
return 0;
return 1;
}
I void link0(const int &_,const int &ii,C a,C &b){
vec d=a.o-b.o;
double t=acos(b.r/d.len());
d=d/d.len()*b.r;
P d1=d.rotate(t),d2=d.rotate(-t);
double len=sqrt((a.o-b.o).len2()-b.r*b.r);
if(check(a.o,b.o+d1,ii))
add(_,b.add(atan2(d1.y,d1.x)),len);
if(check(a.o,b.o+d2,ii))
add(_,b.add(atan2(d2.y,d2.x)),len);
}
I void link1(const int &ja,const int &jb,C &a,C &b){
vec d=a.o-b.o;
if(abs(d.len()-a.r-b.r)<eps)
add(a.add(atan2(-d.y,-d.x)),b.add(atan2(d.y,d.x)),0);
else{
double t=acos((a.r+b.r)/d.len()),l=sqrt(d.len2()-(a.r+b.r)*(a.r+b.r));
d=d/d.len();
vec d1=d.rotate(t)*b.r,d2=d.rotate(-t)*b.r;
d=d*(-1);
vec d3=d.rotate(t)*a.r,d4=d.rotate(-t)*a.r;
if(check(a.o+d3,b.o+d1,ja,jb))
add(a.add(atan2(d3.y,d3.x)),b.add(atan2(d1.y,d1.x)),l);
if(check(a.o+d4,b.o+d2,ja,jb))
add(a.add(atan2(d4.y,d4.x)),b.add(atan2(d2.y,d2.x)),l);
}
d=a.o-b.o;
double t=acos((b.r-a.r)/d.len()),l=sqrt(d.len2()-(b.r-a.r)*(b.r-a.r));
d=d/d.len();
vec d1=d.rotate(t),d2=d.rotate(-t);
if(check(a.o+d1*a.r,b.o+d1*b.r,ja,jb))
add(a.add(atan2(d1.y,d1.x)),b.add(atan2(d1.y,d1.x)),l);
if(check(a.o+d2*a.r,b.o+d2*b.r,ja,jb))
add(a.add(atan2(d2.y,d2.x)),b.add(atan2(d2.y,d2.x)),l);
}
I void link2(C&a){
FOR(i,1,a.tot)v[i]=D(a.id[i],a.pos[i]);
sort(v+1,v+1+a.tot);
v[a.tot+1]=v[1];v[a.tot+1].pos+=2*pi;
FOR(i,1,a.tot)add(v[i].id,v[i+1].id,(v[i+1].pos-v[i].pos)*a.r);
}
int in[M];double d[M];
struct Q{
int key;double value;
I Q(const int &_key=0,const double &_value=0):key(_key),value(_value){}
I bool operator<(const Q&a)const{return value>a.value;}
};
priority_queue<Q>q;
double dijkstra(){
FOR(i,2,idt)d[i]=1e10;
for(q.push(Q(1,d[1]=0));!q.empty();){
Q tmp=q.top();q.pop();
if(in[tmp.key])continue;
in[tmp.key]=1;
for(int i=head[tmp.key];i;i=e[i].nxt)
if(d[e[i].to]>d[tmp.key]+e[i].v)
q.push(Q(e[i].to,d[e[i].to]=d[tmp.key]+e[i].v));
}
return d[2];
}
signed main(){
scanf("%lf%lf%lf%lf%d",&s.o.x,&s.o.y,&t.o.x,&t.o.y,&n);
s.r=t.r=0;
FOR(i,1,n)
scanf("%lf%lf%lf",&cir[i].o.x,&cir[i].o.y,&cir[i].r),
tmp[i].o=cir[i].o,tmp[i].r=cir[i].r,tmp[i].id=i;
if(check(s.o,t.o))add(1,2,(s.o-t.o).len());
FOR(i,1,n)
link0(1,i,s,cir[i]),link0(2,i,t,cir[i]);
FOR(i,1,n){
base=cir[i].o;
sort(tmp+1,tmp+1+n);
ROF(j,n,i+1){
if(cir[i].r<=cir[j].r)link1(i,j,cir[i],cir[j]);
else link1(j,i,cir[j],cir[i]);
}
}
FOR(i,1,n)link2(cir[i]);
printf("%.1lf\n",dijkstra());
return 0;
}
显然这是一个披着计算几何皮的码力题
关于代码冗余:
开float即可,double没必要,题目要求的精度没有那么高;
eps设置的毫无意义;
比较半径大小好像也没有必要;(sort&link1)
后记:
本文写于北京时间2020年2月29日21时59分,也是我的第一篇计算几何的笔记(此时并不会维护凸包)。
代码参考了uoj上的提交记录(自己码力不够),绘图参考了罗哲正的课件。
祝自己,也祝大家再OI的路上越走越走吧( ̄▽ ̄)*
——luxin